欧几里得在《几何原本》中系统化了几何学体系，欧几里得明确描述了二维和三维空间中的距离计算（即勾股定理），但并未直接给出高维推广（因为古希腊数学没有“高维空间”的概念）。现代数学将勾股定理自然推广到 NN 维空间，形成了今天的欧几里得距离公式，但这一推广是后人对欧氏几何的扩展，而非欧几里得本人的工作。欧几里得的贡献在于用公理化方法建立了几何体系。

空间两点之间直线距离的计算公式的思想源于欧几里得几何，后人为了纪念其贡献而命名为 欧几里得距离。

欧几里得距离的定义

对于 NN 维空间中的两点：

• A=(a1,a2,…,aN)A=(a1​,a2​,…,aN​)
• B=(b1,b2,…,bN)B=(b1​,b2​,…,bN​)

它们之间的欧几里得距离（直线距离）公式为：

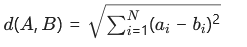
这一公式是两点坐标差值平方和的平方根，假设你用直尺上测量这两个空间点的直线距离，用这个公式只要计算就可以了。

在N维欧几里得空间中，给定两点A(a₁,a₂,…,a_N)和B(b₁,b₂,…,b_N)，它们之间的直线距离可以通过以下公式计算：

d(A,B) = √[(a₁-b₁)² + (a₂-b₂)² + … + (a_N-b_N)²]

这个公式实际上是对勾股定理在N维空间的自然推广。具体来说：

在二维情况下，这就是我们熟知的勾股定理c=√(a²+b²)
在三维情况下，公式扩展为d=√(x²+y²+z²)
在更高维度中，这个规律依然成立